JSTSC 2018滚粗记

发表于 2018-05-04 | 更新于 2018-09-03 | 分类于游记

JSTSC 2018滚粗记

Day 1

T1

第一眼：what???一上来就图论???
后来看看：嗯…好像这个数据范围…
10分肯定是到手了…
（突然看到一条链的情况）
这个条件很诱人耶要不要来做着试试？
话说这题应该是个dp事实上它也就是个dp然后开始推一条链的方程
结果:
???????

什么鬼…
算了算了，这道题已经磕了2个小时了还是看看下一题吧..

阅读全文 »

单调栈

发表于 2018-05-01 | 更新于 2018-09-03 | 分类于讲解

题外话
2333感觉uups里面真的是愈发有趣、有趣得一塌糊涂不可收拾
点击加入群聊【科技区UP主抱团交流群】
欢迎入坑参与身♂心♂愉悦的聊天

单调栈

定义

单调递增或单调减的栈，只用到它的一端，利用它可以用来解决一些ACM/ICPC和OI的题目，如RQNOJ 的诺诺的队列等。

假设如下是一个栈内元素的排列情况(单调递增的栈)：
$1 \rightarrow 2 \rightarrow 4 \rightarrow6$
此时插入情况有两种：
(1)插入元素大于栈顶元素
当插入$7$时，因$7 > 6$，满足单调递增的条件，故可以直接加入栈
此时：
$1\rightarrow 2 \rightarrow 4 \rightarrow 6 \rightarrow 7$
(2)插入的元素小于栈顶元素
当插入$3$时，为了满足单调递增栈的性质，需要先将栈顶的$4,6$弹出，再插入
此时
$1\rightarrow 2\rightarrow 4$
$1 \rightarrow 2$
$1 \rightarrow 2\rightarrow 3$

阅读全文 »

『BZOJ 1935』[SHOI2007]Tree 园丁的烦恼

发表于 2018-04-15 | 更新于 2018-09-15 | 分类于题解

Problem

题目描述 Description
很久很久以前，在遥远的大陆上有一个美丽的国家。统治着这个美丽国家的国王是一个园艺爱好者，在他的皇家花园里种植着各种奇花异草。有一天国王漫步在花园里，若有所思，他问一个园丁道：
“最近我在思索一个问题，如果我们把花坛摆成六个六角形，那么……”
“那么本质上它是一个深度优先搜索，陛下”，园丁深深地向国王鞠了一躬。
“嗯……我听说有一种怪物叫九头蛇，它非常贪吃苹果树……”
“是的，显然这是一道经典的动态规划题，早在N元4002年我们就已经发现了其中的奥秘了，陛下”。
“该死的，你究竟是什么来头？”
“陛下息怒，干我们的这行经常莫名其妙地被问到和OI有关的题目，我也是为了预防万一啊！”
王者的尊严受到了伤害，这是不可容忍的。看来一般的难题是难不倒这位园丁的，国王最后打算用车轮战来消耗他的实力：

“年轻人，在我的花园里的每一棵树可以用一个整数坐标来表示，一会儿，我的骑士们会来轮番询问你某一个矩阵内有多少树，如果你不能立即答对，你就准备走人吧！”说完，国王气呼呼地先走了。

这下轮到园丁傻眼了，他没有准备过这样的问题。所幸的是，作为“全国园丁保护联盟”的会长——你，可以成为他的最后一根救命稻草。

输入描述 Input Description
文件的第一行有两个整数n，m（0≤n≤500000，1≤m≤500000）。n代表皇家花园的树木的总数，m代表骑士们询问的次数。
文件接下来的n行，每行都有两个整数xi，yi，代表第i棵树的坐标（0≤xi，yi≤10000000）。
文件的最后m行，每行都有四个整数aj，bj，cj，dj，表示第j次询问，其中所问的矩形以（aj，bj）为左下坐标，以（cj，dj）为右上坐标。

输出描述 Output Description
共输出m行，每行一个整数，即回答国王以（aj，bj）和（cj，dj）为界的矩形里有多少棵树。

样例输入 Sample Input
3 1
0 0
0 1
1 0
0 0 1 1

样例输出 Sample Output
3

数据范围及提示 Data Size & Hint
0≤n≤500000，1≤m≤500000

Solution

所以说，这道题目第一眼看上去是二维树状数组
但是再看看数据范围太大了，想到离散化
离散化处理还是比较妙的，我们离线找答案，按横坐标排序依次处理。
不能用二维树状数组做（尽管带差分然而仍然会炸），于是就直接按两倍的N建立树状数组来做就行了。
代码跑得很快，洛谷632ms, 暂时Rank1;
然而BZOJ的老机子实在是巨慢无比，居然跑了3300ms左右
结果就Rank n了。
代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <vector>
#define MAXN 2500000 + 5

using namespace std;
int N, M;
struct node
{
	int x, y, flag, num;
};
node a[MAXN];
inline bool cmp(node q, node w)
{
	if (q.x < w.x) return true;
	else
		if (q.x == w.x) return q.num < w.num;
	return false;
}
int t[MAXN], ans[MAXN];
inline int lowbit(int x)
{
	return x & (-x);
}
inline void add(int k)
{
	for (register int i = k; i <= 2 * N; i += lowbit(i)) ++t[i];
}
inline int query(int k)
{
	int res = 0;
	for (register int i = k; i > 0; i -= lowbit(i))
		res += t[i];
	return res; 
}
inline char nc()
{
	static char buf[100000], *p1 = buf, *p2 = buf;
	return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000, stdin), p1 == p2) ? EOF : *p1++;
}
inline int _read()
{
	int a = 0, f = 1;
	static char c = nc();
	while (c < '0' || c > '9')
	{
		if (c == '-') f = -1;
		c = nc();
	}
	while (c >= '0' && c <= '9')
	{
		a = a * 10 + c - '0';
		c = nc();
	}
	return a * f;
}

int main(int argc, char **argv)
{
	N = _read(), M = _read();
	for (register int i = 1; i <= N; ++i)
	{
		a[i].x = _read(), a[i].y = _read(); 
		a[i].x++, a[i].y++;
		a[i].num = a[i].num = 0;
	}
	int now = N;
	for (register int i = 1; i <= M; ++i)
	{
		int x1, x2, y1, y2;
		x1 = _read(), y1 = _read(), x2 = _read(), y2 = _read();
		a[++now] = (node){x1, y1, 1, i};
		a[++now] = (node){x2 + 1, y2 + 1, 1, i};
		a[++now] = (node){x1, y2 + 1, -1, i};
		a[++now] = (node){x2 + 1, y1, -1, i};
	}
	sort(a + 1, a + now + 1, cmp);
	for (register int i = 1; i <= now; ++i)
		if (!a[i].num)
		{
			add(a[i].y);
		}
		else
		{
			ans[a[i].num] += a[i].flag * query(a[i].y);
		}
	for (register int i = 1; i <= M; ++i)
		printf("%d\n", ans[i]);
	return 0;
}

~~话说为了Rank1我tm第一次写了fread的读入优化啊。。~~

『洛谷 P1706』全排列

发表于 2018-03-31 | 更新于 2018-09-15 | 分类于题解

辣鸡题目。直接STL水掉，84ms AC

#include <iostream>
#include <algorithm>
using namespace std;
int a[10], N;
int main(int argc, char **argv)
{
	ios::sync_with_stdio(false);
	cin >> N;
	for (register int i = 1; i <= N; ++i) a[i] = i, cout << "    " << i;
	cout << endl;
	while (next_permutation(a + 1, a + N + 1))
	{
		for (register int i = 1; i <= N; ++i)
			cout << "    " << a[i];
		cout << endl;
	}
	return 0;
}

求乘法逆元

发表于 2018-03-31 | 分类于讲解

两种方法

拓展欧几里得法

证明不再赘述，直接上我的代码——

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
typedef long long ll;
using namespace std;
inline void exgcd(ll a, ll b, ll &d, ll &x, ll &y)
{
	if (!b) d = a, x = 1, y = 0;
	else exgcd(b, a % b, d, y, x), y -= x * (a / b);
}
inline ll inv(ll a, ll p)
{
	ll d, x, y;
	exgcd(a, p, d, x, y);
	return d == 1 ? (x + p) % p : -1;
}
int main(int argc, char **argv)
{
	ll a, b;
	cin >> a >> b;
	cout << inv(a, b) << endl;
	return 0;
}

求的是ax≡1(mod p)的逆元

费马小定理法

lyj的代码

#include <cstdio>
using namespace std;

const int p = 1e9 + 7;

int power(int a, int b)
{
	int ans = 1;
	for (; b; (a *= a) %= p, b >>= 1)
		if (b & 1) (ans *= a) %= p;
	return ans % p;
}

int main()
{
	int a;
	scanf("%d", &a);
	printf("%d\n", power(a, p - 2));
}

『洛谷 P1026』第K小数

发表于 2018-03-30 | 更新于 2018-09-15 | 分类于题解

水一波题解。。
~~我不会告诉你我没看见输出NO RESULT所以WA了两次。。。~~

#include <iostream>
#include <cstdio>
#include <algorithm>
#define MAXN 10000 + 1
using namespace std;
int N, k;
int a[MAXN];
int main(int argc, char **argv)
{
	ios::sync_with_stdio(false);
	cin >> N >> k;
	for (register int i = 1; i <= N; ++i)
		cin >> a[i];
	sort(a + 1, a + N + 1);
	if (k == 1)
	{
		cout << a[1] << endl;
		return 0;
	}
	int kth = 1;
	for (register int i = 2; i <= N; ++i)
	{
		if (a[i] != a[i - 1]) kth++;
		if (kth == k)
		{
			cout << a[i] << endl;
			return 0;
		}
	}
	cout << "NO RESULT" << endl;
	return 0;
}

『洛谷 P1510』精卫填海

发表于 2018-03-28 | 更新于 2018-09-15 | 分类于题解

Problem

问题描述

发鸠之山，其上多柘木。有鸟焉，其状如乌，文首，白喙，赤足，名曰精卫，其名自詨。是炎帝之少女，名曰女娃。女娃游于东海，溺而不返，故为精卫。常衔西山之木石，以堙于东海。——《山海经》

精卫终于快把东海填平了！只剩下了最后的一小片区域了。同时，西山上的木石也已经不多了。精卫能把东海填平吗？

事实上，东海未填平的区域还需要至少体积为v的木石才可以填平，而西山上的木石还剩下n块，每块的体积和把它衔到东海需要的体力分别为k和m。精卫已经填海填了这么长时间了，她也很累了，她还剩下的体力为c。

阅读全文 »

『HDU 3068』最长回文

发表于 2018-03-27 | 更新于 2018-09-15 | 分类于题解

Problem

Problem Description
给出一个只由小写英文字符a,b,c…y,z组成的字符串S,求S中最长回文串的长度.
回文就是正反读都是一样的字符串,如aba, abba等

Input
输入有多组case,不超过120组,每组输入为一行小写英文字符a,b,c…y,z组成的字符串S
两组case之间由空行隔开(该空行不用处理)
字符串长度len <= 110000

Output
每一行一个整数x,对应一组case,表示该组case的字符串中所包含的最长回文长度.

Sample Input
aaaa
abab

Sample Output
4
3

Solution

这道题是一道Manachar模板题

Manacher

背景

解决的问题就是：
给定一个字符串，求出其最长回文子串。例如：

s=”abcd”,最长回文长度为 1；
s=”ababa”,最长回文长度为 5；
s=”abccb”,最长回文长度为 4，即 bccb。
以上问题的传统思路大概是，遍历每一个字符，以该字符为中点向两边查找。其时间复杂度为O(n^2)，很不高效，但这个思想我们下面要用到。而在1975年，一个叫Manacher的人发明了一个算法，该算法可以把时间复杂度提升到O(n)。下面来看看该算法是如何工作的。

算法过程

由于回文分为偶回文（比如 bccb）和奇回文（比如 bcacb），而在处理奇偶问题上会比较繁琐，所以这里我们使用一个技巧，在字符间插入一个字符（前提这个字符未出现在串里）。举个例子：s=abbahopxpo转换为s_new=$#a#b#b#a#h#o#p#x#p#o#（这里的字符 $; 只是为了防止越界，下面代码会有说明），如此，字符串s里起初有一个偶回文abba和一个奇回文opxpo，被转换为#a#b#b#a#和-#o#p#x#p#o#，长度都转换成了奇数。

定义一个辅助数组p，p[i]表示以snew[i]为中心的最长回文的半径，例如：

可以看出，p[i]-1正好是原字符串中最长回文串的长度。
Manacher算法之所以快，就快在对 p 数组的求法上有个捷径。在我们解决了奇偶回文的繁琐时，剩下的难点就是求 p 数组，按照普通思维，我们是这样求解的：求解p[i]，先初始化p[i]=1，再以snew[i]为中心判断两边是否相等，相等就将p[i]+1。这就是之前我们提到的传统思路，但是我们想想，能否让p[i]的初始化不是 1，让它更大点，看下图：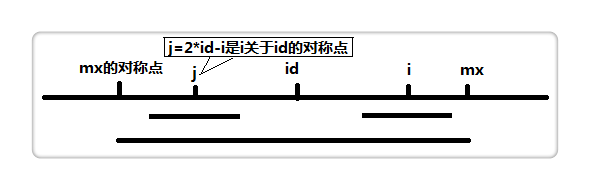

于是我们可以这样解决：
设置两个变量，maxpos 和 id 。maxpos 代表以snew[id]为中心的最长回文最右边界，即为maxpos=id+p[id]。
假设我们现在求p[i]，也就是以snew[i]为中心的最长回文半径，如果i < maxpos，如上图，那么p[i] = min(p[2 id - i], mx - i)
2 id - i其实就是等于 j ，p[j]表示以s_new[j]为中心的最长回文半径，见上图，因为 i 和 j 关于 id 对称，我们利用p[j]来加快查找。

复杂度分析

这样看起来很暴力，为什么复杂度是O(n)的呢？因为maxpos不会减小，每次暴力处理的时候，p[i]增大多少，就说明maxpos增大多少，而maxpos最多增加len次。所以复杂度是O(n)的。

代码

代码值得注意的是，p数组和snew数组务必要是字符串原串长度的两倍！不然会莫名TLE！

#include <iostream>
#include <string>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#define MAXN 110000 + 10
using namespace std;
char s[MAXN], snew[2 * MAXN];
int p[2 * MAXN];
inline int Init()
{
	int len = strlen(s);
	snew[0] = '$';		//防止在前面越界
	snew[1] = '#';
	int j = 2;
	for (register int i = 0; i < len; ++i)
	{
		snew[j++] = s[i];
		snew[j++] = '#';
	}
	snew[j] = '\0';		//防止在后面越界
	return j;
}
inline int Manacher()
{
	int maxlen = -1, len = Init();
	int id, maxpos = 0;
	for (register int i = 1; i < len; ++i)
	{
		if (i < maxpos) p[i] = min(p[id * 2 - i], maxpos - i);
		else p[i] = 1;
		while (snew[i - p[i]] == snew[i + p[i]]) p[i]++;
		if (maxpos < i + p[i])
			id = i, maxpos = i + p[i];
		maxlen = max(maxlen, p[i] - 1);
	}
	return maxlen;
}
int main(int argc, char **argv)
{
	ios::sync_with_stdio(false);
	while (cin >> s) cout << Manacher() << endl;
	return 0;
}

『BZOJ 1588』 [HNOI2002]营业额统计

发表于 2018-03-26 | 更新于 2018-09-15 | 分类于题解

Problem

Description
营业额统计 Tiger最近被公司升任为营业部经理，他上任后接受公司交给的第一项任务便是统计并分析公司成立以来的营业情况。 Tiger拿出了公司的账本，账本上记录了公司成立以来每天的营业额。分析营业情况是一项相当复杂的工作。由于节假日，大减价或者是其他情况的时候，营业额会出现一定的波动，当然一定的波动是能够接受的，但是在某些时候营业额突变得很高或是很低，这就证明公司此时的经营状况出现了问题。经济管理学上定义了一种最小波动值来衡量这种情况：该天的最小波动值当最小波动值越大时，就说明营业情况越不稳定。而分析整个公司的从成立到现在营业情况是否稳定，只需要把每一天的最小波动值加起来就可以了。你的任务就是编写一个程序帮助Tiger来计算这一个值。第一天的最小波动值为第一天的营业额。  输入输出要求

Input
第一行为正整数，表示该公司从成立一直到现在的天数，接下来的n行每行有一个整数(有可能有负数) ，表示第i
天公司的营业额。
天数n<=32767,
每天的营业额ai <= 1,000,000。
最后结果T<=2^31
Output
输出文件仅有一个正整数，即Sigma(每天最小的波动值) 。结果小于2^31 。

Sample Input
6
5
1
2
5
4
6

Sample Output
12

HINT
结果说明：5+|1-5|+|2-1|+|5-5|+|4-5|+|6-5|=5+4+1+0+1+1=12

Solution

模板splay题
而且不带删除的
发现splay静态的写法比动态的写法好很多：代码复杂度小，而且更快
本蒟蒻代码运行结果：
Accepted 2844 kb 724 ms C++/Edit 1971 B
表示不是很懂那些几十ms是怎么刷出来的？（也许那时候BZOJ的评测机比较快）

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <iostream>
#define MAXN 100010
#define inf (1<<30)
using namespace std;
int fa[MAXN], t[MAXN][2], val[MAXN];
int n, size, root = 0, x1, x2;
inline void Rotate(int x, int &k)
{
	int y = fa[x], z = fa[y], l, r;
	if (t[y][0] == x) l = 0; else l = 1;
	r = l ^ 1;
	if (k == y) k = x;		//如果要旋转到的节点已经是它的父节点，就将要旋转到的节点(通常是根)改为x 
	else t[z][t[z][1] == y] = x;		//如果z的右孩子是y，那么就将右孩子改为x，否则将左孩子改为x，右孩子不变 
	fa[x] = z, fa[y] = x;
	fa[t[x][r]] = y; 
	t[y][l] = t[x][r];
	t[x][r] = y;
}
inline void Splay(int x, int &k) 
{
	while (x != k)
	{
		int y = fa[x], z = fa[y];
		if (y != k)
		{
			(t[y][0]==x) ^ (t[z][0]==y) ? Rotate(x, k) : Rotate(y, k);
		}
		Rotate(x, k);
	}
}
inline bool ins(int &k, int x, int f)
{
	if (!k)
	{
		k = ++size;
		val[k] = x, fa[k] = f, Splay(k, root);
		return 1;
	}
	if (val[k] == x) return 0; 
	if (x < val[k]) return ins(t[k][0], x, k);
	else return ins(t[k][1], x, k);
}
inline void pred(int k)
{
	if (!t[k][0]) return ;
	k = t[k][0];
	while (t[k][1]) k = t[k][1];
	x1 = val[k];
}
inline void succ(int k)
{
	if (!t[k][1]) return ;
	k = t[k][1];
	while (t[k][0]) k = t[k][0];
	x2 = val[k];
}
int main(int argc, char **argv)
{
	ios::sync_with_stdio(false);
	int N;
	int ans = 0;
	cin >> N;
	for (register int i = 1; i <= N; ++i)
	{
		int x;
		cin >> x;
		if (!ins(root, x, 0)) continue;
		x1 = -inf, x2 = inf;
		if (i == 1) ans += x;
		else
		{
			pred(root), succ(root);
			ans += min(abs(x - x1), abs(x2 - x));
		}
	}
	cout << ans << endl; 
	return 0;
}

『BZOJ 4520』[CQOI2016]K远点对

发表于 2018-03-22 | 更新于 2018-09-15 | 分类于题解

Problem

Description
已知平面内 $N$ 个点的坐标，求欧氏距离下的第 $K$ 远点对。

Input
输入文件第一行为用空格隔开的两个整数$ N, K$。接下来$ N$ 行，每行两个整数 $X,Y$，表示一个点
的坐标。$1 \leq N \leq 100000， 1 \leq K \leq 100， K \leq \dfrac{N (N−1)}{2} ， 0 \leq X, Y < 2^31$。

Output
输出文件第一行为一个整数，表示第 $K $远点对的距离的平方（一定是个整数）。

Sample Input
10 5
0 0
0 1
1 0
1 1
2 0
2 1
1 2
0 2
3 0
3 1
Sample Output
9

Solution

这题是KDTree模板题啊Orzzz
然额本蒟蒻打了好久才调出来
原因：

简直了。。
附上蒟蒻代码：（太懒没时间打注释）
跑的实在是巨慢：

顺便说一句：那个MAX和MIN记录的是当前矩阵区域内最大的横纵坐标值

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#include <queue>
#include <cmath>
#define MAXN 100011
int N, K, nowD, root, ql, qr; 
using namespace std;
struct node
{
	long long dis;
	inline bool operator < (const node &a) const
	{
		return a.dis < dis;
	}
};
typedef struct KDTree
{
	int d[2], Min[2], Max[2], l, r;
} KDT;
KDT Tree[MAXN];
priority_queue <node> Q;
inline long long sqr(long long a)
{
	return a * a;
}
inline void MAX(KDT &a, KDT b, int type)
{
	a.Max[type] = max(a.Max[type], b.Max[type]);
}
inline void MIN(KDT &a, KDT b, int type)
{
	a.Min[type] = min(a.Min[type], b.Min[type]);
}
inline long long GetDis(int x, int y)
{
	return sqr(Tree[x].d[0] - Tree[y].d[0]) + sqr(Tree[y].d[1] - Tree[x].d[1]);
}
inline bool cmp(KDT a, KDT b)
{
	if (a.d[nowD] == b.d[nowD])
	{
		return a.d[nowD ^ 1] < b.d[nowD ^ 1];
	}
	else
	return a.d[nowD] < b.d[nowD];
}
inline void Update(int x)
{
	if (Tree[x].l) for (register int i = 0; i < 2; ++i) MAX(Tree[x], Tree[Tree[x].l], i), MIN(Tree[x], Tree[Tree[x].l], i);
	if (Tree[x].r) for (register int i = 0; i < 2; ++i) MAX(Tree[x], Tree[Tree[x].r], i), MIN(Tree[x], Tree[Tree[x].r], i);
}
inline int Build(int l, int r, int D)
{
	nowD = D;
	int mid = (l + r) >> 1;
	nth_element(Tree + l + 1, Tree + mid + 1, Tree + r + 1, cmp);
	if (l < mid) Tree[mid].l = Build(l, mid - 1, D ^ 1);
	if (mid < r) Tree[mid].r = Build(mid + 1, r, D ^ 1);
	for (register int i = 0; i < 2; ++i)
		Tree[mid].Min[i] = Tree[mid].Max[i] = Tree[mid].d[i];
	Update(mid);
	return mid;
}
inline long long Adis(KDT A, KDT B)
{
	return max(sqr(A.d[0] - B.Min[0]), sqr(A.d[0] - B.Max[0])) + max(sqr(A.d[1] - B.Min[1]), sqr(A.d[1] - B.Max[1]));
}
inline void Query(int x)
{
	long long dl = 0, dr = 0;
	long long dis = GetDis(0, x);
	if (dis > Q.top().dis)
	{
		Q.pop();
		Q.push((node){ dis });
	}
	if (Tree[x].l) dl = Adis(Tree[0], Tree[Tree[x].l]);
	if (Tree[x].r) dr = Adis(Tree[0], Tree[Tree[x].r]);
	if (dl > dr)
	{
		if (dl > Q.top().dis) Query(Tree[x].l);
		if (dr > Q.top().dis) Query(Tree[x].r);
	}
	else
	{
		if (dr > Q.top().dis) Query(Tree[x].r);
		if (dl > Q.top().dis) Query(Tree[x].l);
	}
}
int main(int argc, char **argv)
{
	ios::sync_with_stdio(false); 
	cin >> N >> K;
	for (register int i = 1; i <= N; ++i)
	{
		cin >> Tree[i].d[0] >> Tree[i].d[1];
	}
	root = Build(1, N, 0);
	for (register int i = 1; i <= K * 2; ++i)
		Q.push((node) { 0 });
	for (register int i = 1; i <= N; ++i)
	{
		Tree[0].d[0] = Tree[i].d[0];
		Tree[0].d[1] = Tree[i].d[1];
		Query(root); 
	}
	cout << Q.top().dis << endl;
	return 0;
}