窗函数
实在是无聊(主要是因为llc神犇在上学期提过窗函数,然而我当时并看不懂,这次把坑填上…)…然后看了几篇关于窗函数的资料…本文就权当抛砖引玉吧
数字信号处理的主要数学工具是傅里叶变换,而傅里叶变换是研究整个时间域和频率域的关系,当运用计算机实现测试信号处理时,不可能对无限长的信号进行测量和运算,而是取其有限的时间片段进行分析。
- 从信号中截取一个时间片段,
然后用截取的信号时间片段进行周期延拓处理,得到虚拟的无限长信号,再进行傅里叶变换和相关分析。无限长信号被截断后,其频谱发生了畸变,我们称为频谱能量泄漏,为了减少频谱泄漏,可采用不同的截取函数对信号进行截断,截断函数称为窗函数,简称为窗。
据学信号学的大佬所说,杠掉的地方有些问题。所以这里展示一下大佬的笔记吧,就不重新表述了(公式太多QwQ)
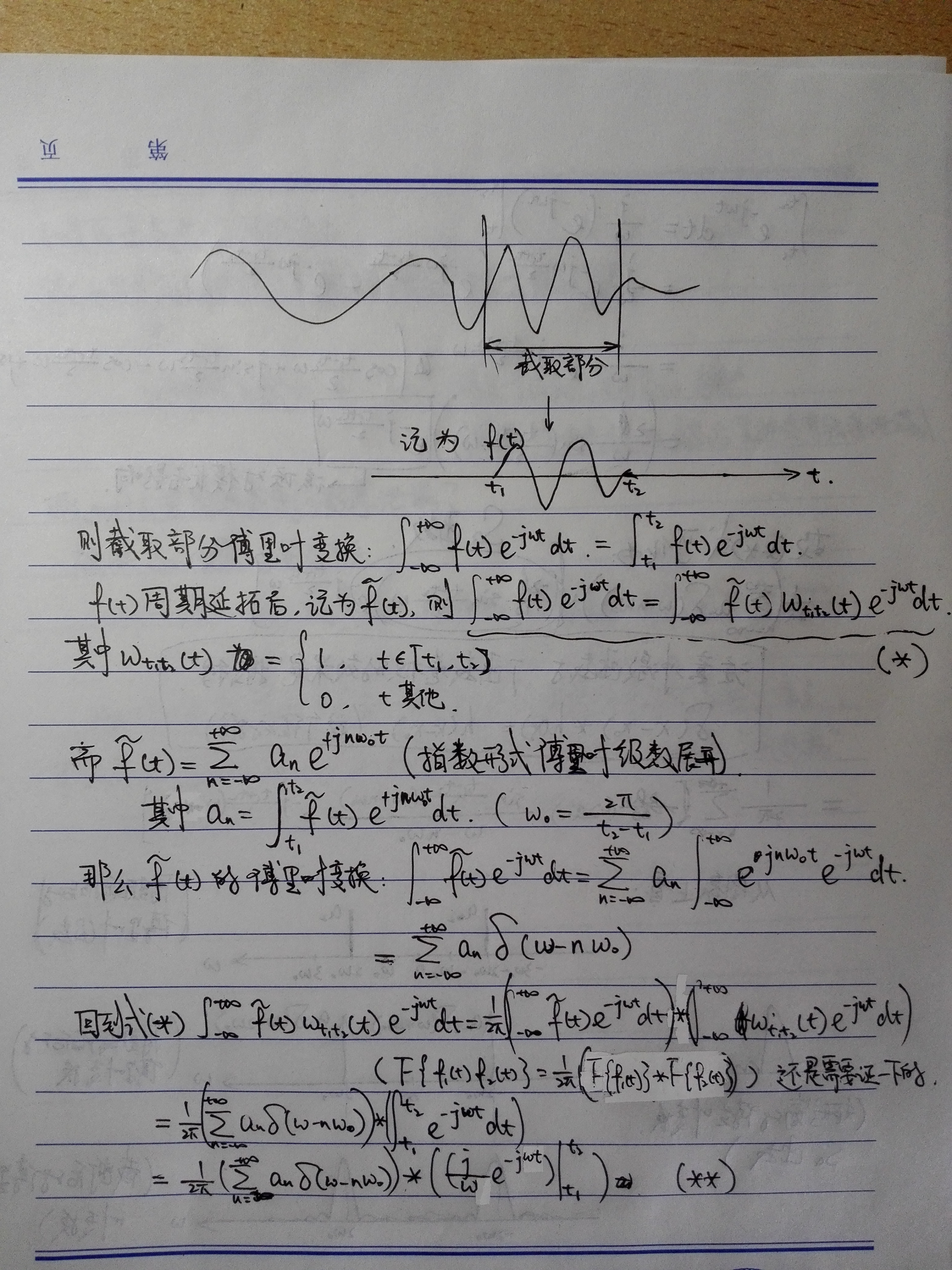


顺便膜一下dalao,看不懂的孩纸还是继续看下文吧
加窗的目的
其实上文已经讲过了,计算机不可能对无限长的信号进行测量和运算。每次$\rm FFT$只能对有限长度的时域数据进行变换,因此需要对时域信号进行信号截断,即使是周期信号,如果截断的时间长度不是周期的整数倍(整周期截断),那么截取后的信号也会存在频谱泄漏,为了将这个泄漏误差减少到最小程度(不是消除),我们需要使用窗函数。加窗主要是为了使时域信号似乎更好的满足$\rm FFT$处理的周期性要求,减少泄漏。
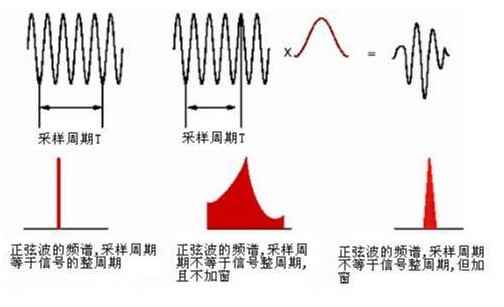
从上图我们得出,如果是整周期截断,则$\rm FFT$频谱为单一谱线。若为非整周期截断,则频谱出现拖尾,也就是说泄漏很严重。为了减少泄漏,给信号施加一个窗函数,原始截断后的信号与这个窗函数相乘之后得到的信号为最右侧的信号。可以看出,此时信号的起始时刻和结束时刻幅值都为$0$,也就是说在这个时间长度内,信号为周期信号,但是只有一个周期,对这个信号做$\rm FFT$,相比之前未加窗的频谱,泄漏已明显改善,但并未完全消除,因此窗函数只能减少泄漏,不能消除泄漏。
窗函数的形象描述
信号截断时,只能截取一定长度,哪怕原始信号是无限长,就好像是用一个窗(确切来说更像一个框)去做这样的截取。如下Pic.1所示,原始信号是周期信号,时间很长,截取时用红色的窗去截取这个周期信号,截取得到的信号如Pic.2所示。
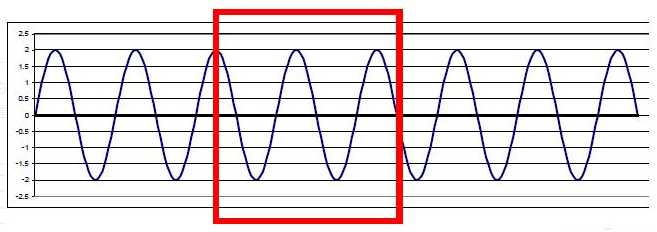
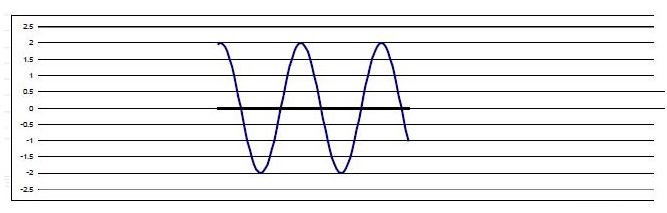
这个“窗”是一个单位权重的加权函数,成为矩形窗。这个窗外的信号是看不到的,就如同透过窗户看外面的世界,你只能看到在窗内的景色。这就是为什么这样的加权函数被成为窗函数的真正原因(其实还是很形象的)。
Pic.2中用于截取信号的时域截取函数称为窗函数,它是一种加权函数,不同窗的加权是不一样的,也就是说,可以用不同的窗函数来做信号截断。常用的窗函数有矩形窗、汉宁窗、平顶窗和指数窗等。
加窗在时域上表现的是点乘,因此在频域上则表现为卷积。卷积可以被看成是一个平滑的过程。这个平滑过程可以被看出是由一组具有特定函数形状的滤波器,因此,原始信号中在某一频率点上的能量会结合滤波器的形状表现出来,从而减小泄漏。基于这个原理,人们通常在时域上直接加窗。
窗函数的时频域特征

上面那幅图当中,较为平缓的曲线为时域形状,有若干个瓣是频域特征
窗函数的典型频谱特征如下图所示:

窗函数的选择
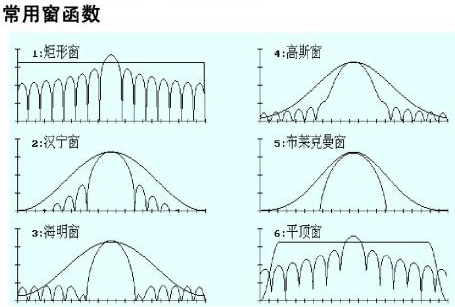
在上面的常用窗函数一图当中,矩形窗主瓣窄,旁瓣大,频率识别精度最高,幅值识别精度最低,如果仅要求精确读出主瓣频率,而不考虑幅值精度,则可选用矩形窗,例如测量物体的自振频率等;布莱克曼窗主瓣宽,旁瓣小,频率识别精度最低,但幅值识别精度最高;如果分析窄带信号,且有较强的干扰噪声,则应选用旁瓣幅度小的窗函数,如汉宁窗、三角窗等;对于随时间按指数衰减的函数,可采用指数窗来提高信噪比。 如果被测信号是随机或者未知的,或者是一般使用者对窗函数不大了解,要求也不是特别高时,可以选择汉宁窗,因为它的泄漏、波动都较小,并且选择性也较高。但在用于校准时选用平顶窗较好,因为它的通带波动非常小,幅度误差也较小。
看一下各种窗函数的对比(好吧其实我不是很懂这个地方,还是需要学习):
| 名称 | 表达式 |
|---|---|
| 矩形窗 | ${\displaystyle w(n)=1}$ |
| 汉宁窗 | ${\displaystyle w(n)=0.5\;\left(1-\cos \left({\frac {2\pi n}{N-1}}\right)\right)}$ |
| 平顶窗 | ${\displaystyle w(n)=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N-1}}\right)+a_{2}\cos \left({\frac {4\pi n}{N-1}}\right)-a_{3}\cos \left({\frac {6\pi n}{N-1}}\right)+a_{4}\cos \left({\frac {8\pi n}{N-1}}\right)}\\a_{0}=1;\quad a_{1}=1.93;\quad a_{2}=1.29;\quad a_{3}=0.388;\quad a_{4}=0.028$ |
| 海明窗 | ${\displaystyle w(n)=0.53836-0.46164\;\cos \left({\frac {2\pi n}{N-1}}\right)}$ |
| Kaiser窗 | ${\displaystyle w(n)={\frac {I_{0}{\Bigg (}\pi \alpha {\sqrt {1-( {\begin{matrix}{\frac {2n}{N-1} }\end{matrix} }-1)^{2} } }{\Bigg ) } }{I_{0}(\pi \alpha ) } } } $ |
| 布莱克曼窗 | ${\displaystyle w(n)=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N-1}}\right)+a_{2}\cos \left({\frac {4\pi n}{N-1}}\right) } \\ a_{0}={\frac {1-\alpha }{2}};\quad a_{1}={\frac {1}{2}};\quad a_{2}={\frac {\alpha }{2} }$ |
| 高斯窗 | ${\displaystyle w(n)=e^{-{\frac {1}{2}}\left({\frac {n-(N-1)/2}{\sigma (N-1)/2}}\right)^{2}}}$ |
| 三角窗 | $\displaystyle w(n)=1 - \text{abs}\left ( {\frac{n-{\frac {N-1}{2} } }{\frac{L}{2} } } \right )$ |
| Chebyshev窗 | ${\displaystyle {\begin{aligned} W_{0}(k)&={\frac {\cos\{N\cos ^{-1}[\beta \cos({\frac {\pi k}{N} } ) ] \} } {\cosh[N\cosh ^{-1}(\beta ) ] } } \\\beta &=\cosh[ {\frac {1}{N} }\cosh ^{-1}(10^{\alpha } ) ],\end{aligned} } }$ |
| 名称 | 特点 | 应用 |
|---|---|---|
| 矩形窗 | 矩形窗使用最多,习惯上不加窗就是使信号通过了矩形窗。这种窗的有点是主瓣集中,缺点是旁瓣比较高,并且有负旁瓣,导致变换中带进了高频干扰和泄露,甚至出现负谱现象。频率识别精度最高,幅值识别精度最低,所以矩形窗并不是非常理想 | 仅要求精确读出主瓣频率,而不考虑幅值精度,则可以使用矩形窗,例如测量物体的自振频率和阶次分析 |
| 汉宁窗 | 又称升余弦窗,可以看作是$3$个矩形时间窗的频谱之和,或者说是$3$个$\text{sinc}(T)$型函数之和。汉宁窗主瓣加宽并降低,旁瓣则显著减小,从减小泄漏观点出发,汉宁窗优于矩形窗.但汉宁窗主瓣加宽,相当于分析带宽加宽,频率分辨力下降。 | 如果测试信号有多个频率分量,频谱表现的十分复杂,且测试的目的更多关注频率点而并非能量的大小,需要选择汉宁窗。如果被测信号是随机的或者未知的也要选择汉宁窗 |
| 平顶窗 | 平顶窗在频域时的表现就像它的名称一样有非常小的通带波动 | 由于在幅度上有较小的误差,这个窗可以用在校准上 |
| 海明窗 | 也是余弦窗,又称改进的升余弦窗,加权系数不同,使得旁瓣达到更小,但旁瓣衰减速度比汉宁窗更慢 | 和汉宁窗类似 |
| Kaiser窗 | 定义了一组可调的由零阶Bessel函数构成的窗函数,通过调整参数$\beta$,可以在主瓣宽度和旁瓣衰减之间自由选择它们的比重。对于某一长度的Kaiser窗,给定$\beta$,则旁瓣高度固定。 | 最好的旁瓣抑制性能 |
| 布莱克曼窗 | 二阶升余弦窗,主瓣宽,旁瓣比较低,但等效噪声贷款比汉宁窗要大一些,波动却小一些。频率识别精度最低,值识别精度最高(和矩形窗刚好相反),有更好的选择性 | 用来检测两个频率相近幅度不同的信号 |
| 高斯窗 | 是一种指数窗。高斯窗谱无负的旁瓣,第一旁瓣衰减达$-55\rm dB$。高斯富谱的主瓣较宽,所以频率分辨力低。 | 截短一些非周期信号,如指数衰减信号等。 |
| 三角窗 | 是幂窗的一次方形式。与矩形窗比较,主瓣宽约等于矩形窗的两倍,但旁瓣小,而且没有负旁瓣。 | 分析有较强干扰噪声的窄带信号(也可用汉宁窗) |
| Chebyshev窗 | 在给定旁瓣高度下,Chebyshev窗的主瓣宽度最小,具有等波动性,就是说其所有的旁瓣都有相等的高度 |
Questions
加窗是为了截取信号的某一截?如果采集了32K的点,点数不是已经有限了?
并不是。
FFT算法基于你采样的信号是无限长的周期的信号,也就是你32k的数据会被认为是不断重复的,32k最后一个点之后又连到第一个点,这样不断重复,这样就有可能出现波形断开的情况,这个不连续会导致FFT结果出现频谱泄漏现象, 但是你的实际信号是连续的,所以加窗的目的就是让不太连续的地方(最后一个点和第一个的连接处)看上去平滑了,没有原来那么明显的突变了
原始数据加窗之后,数据都变了,FFT后的频谱为什么还能作为参考?
这个问题其实非常的奇怪…
窗函数加在时间域上,相当于和信号做乘法,所以频域上是卷积,这就是傅里叶变换的性质
窗函数不是周期函数。它的频率可以看成无穷小,傅里叶变换从另一个角度也可以看成傅里叶级数当T趋于无穷的极限。
加完窗到底能改进些什么?当然是减少能量泄露。因为不加窗无穷序列,计算机没法做FFT,加窗是迫不得已。有的时候你想了解某一段的频率特性,也需要加窗。加窗的影响就是那个卷积变换,自己要加入幅值修正。
Related
[1] WIKIPEDIA, Window Function
[2] VFE, 通俗地理解窗函数
[3] 雪韵凌枫, 数字信号分析——窗函数
