基础乐理与数学(二)
Read before
阅读本文之前,您先需要阅读基础乐理与数学(一)
五线谱进阶
五线谱中的相对音程
上一讲我们已经知道了高音五线谱中,第二间的$A$的音高定为$440\rm Hz$,很自然地引出了一个问题,我们如何来确定其它音的音高?下面将会按照十二平均律的法则在五线谱中建立相对音高系统。

上图是一个放大的最简单的高音谱,可以看到第一线上的音名是$E$,第一间的音名是$F$,其它以此类推。右侧的全和半表示相邻两个音符之间的音程是全音还是半音。至于为什么是这样规定的,会在下一节进一步展开。确定了音符之间的相对音程,并确定了一个基准音高$A$,我们就可以开始推算所有其它单音的频率了。
首先为了方便的表示众多音符,下文将使用科学记音法(详见维基百科)来表示所有的音符,即两个字符表示一个音:$XN$。其中$X$为音名,可以是$\{C, D, E, F, G, A, B\}$中的任意一个;$N$为该音的序号,从$0$开始由低到高编号。$N$每增加$1$,音的频率就翻倍,并规定第$C4$位于高音五线谱的下加一线。根据科学音调记号法,高音谱下加一线上的$C$记作$C4$,往高依次是$D4,E4,F4……$往低依次是$B3,A3,G3……$。所有的$C$音在五线谱上标记,如下图所示。

比$A4$低纯八度的音符是$A3$,其频率为A4频率的一半,即$220\rm Hz$,比$A4$高纯八度的音符是$A5$,频率为$A4$频率的二倍,即$880$。$A0$到$A7$间所有$A$音的频率见下表:
| 基准音名 | A0 | A1 | A2 | A3 | A4 | A5 | A6 | A7 |
|---|---|---|---|---|---|---|---|---|
| 频率$(\rm Hz)$ | $27.5$ | $55$ | $110$ | $220$ | $440$ | $880$ | $1760$ | $3520$ |
要计算其它音符$XN$的频率$f_X$,则应以$XN$下方的第一个$A$音$AN’$的频率$f_A$作为基准,然后算出$XN$与$AN’$之间的音数$t$,那么$XN$的频率为:$\displaystyle f_X=f_A\times 2^\frac{2t}{12}=f_A\times 2^\frac{t}{6}$。例如,由于第三间的$C$音(即$C5$)与其下方第一个$A$音,即$A4$之间的音程是小三度,音数$t=1.5$,因此$C5$的频率为:$\displaystyle 440\times 2^\frac{1.5}{6}\approx 523.25113\text{Hz}$。当然,也可通过纯八度音程的倍率关系计算,比如$C4$的频率为$C5$的$\dfrac{1}{2}$,约为$261.62557 \rm Hz$。
升降记号
五线谱中,音符的后面可以添加升降标记,表示该音符升高半音或降低半音。升号为#,降号为b。显然,有两个音是没必要升的:$E$升半音就是$F$,$B$升半音就是$C$,而这就是钢琴键盘布局形成的原因。如下图所示:
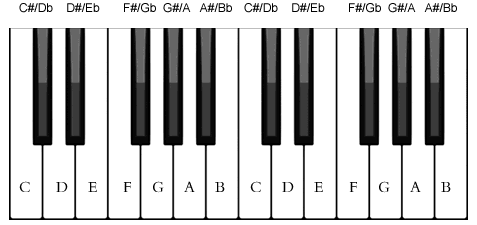
钢琴上的黑键比左边的白键高半音(也可以说是比右边的白键低半音),因此白键$B$和$E$的右边就没有黑键。此外,所有的降音都可以由另一些音的升音代替,比如$B$b就是$A$#,$G$b就是$F$#。那既然如此,为什么不用升号代替全部的降号呢?原因就是为了可读性,正如写代码时不能为了减少代码量就把所有的if语句都换成三目运算符。
如果一段谱子中的某个音符几乎都要升半音或降半音处理,那就可以在高音谱号的右侧,这个音符所在的一条线或一个间上标记升降号。
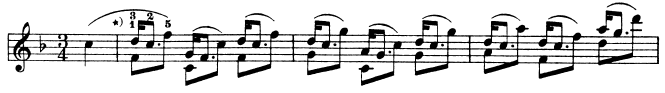
在上图乐谱中,第三线上标记了一个降号b,表示这个谱子里的所有$B$音都需降半音,除非另外在个别音符上标记升降或还原记号。音符被升降半音后的频率可根据之前学过的相邻音符之间的频率倍数关系计算。升高半音后的频率为原频率的$\sqrt[12]{2}$倍,降低半音后的频率为原频率的$\dfrac{1}{\sqrt[12]{2}}$倍。比如$C5$升高半音的频率即为$523.25113\times \sqrt[12]{2}\approx 554.3653\text{Hz}$。
双音谱

是一个钢琴谱,这下我们终于见到了高音谱号和低音谱号并存的样子了。标有高音谱号的上面一排是高音谱,标有低音谱号的下面一排是低音谱,它们分别对应钢琴健盘上不同的键区。低音谱的线和$间$所对应的音符与高音谱不同,如下图:
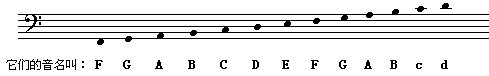
低音谱实际上是和高音谱互相连接的,音名也没有那么难记,中间刚好只隔了一条加线。高音谱的下加一线就是低音谱的上加一线,而这条线上的音就是中央$C$,即$C4$。和高音谱号类似,低音谱号的圆心标记的是$F3$在谱中的位置,即第四线上。
低音谱中各音的频率计算与高音谱是相同的,只要搞清音程关系,从基准音推算即可。比如在前面的钢琴谱中可以看到低音谱的最左端有两个$C$(是用圆圈表示),一个是第二间的$C3$;另一个是下加二线上的$C2$。$C3$和$C2$的频率分别为$C4$频率的$\dfrac{1}{4}$和$\dfrac{1}{8}$,而$C4$的频率在前面已经计算过了。
利用上面的知识,你已经可以计算任何一个五线谱中每个音的频率了,接下来我们介绍对一些特别的频率进行合成的问题——和声。
和声
和声,是指由超过一个单音所组合而成的声音。你可能会发现,和声的定义与拍音的定义是非常相似的。的确如此,所有的拍音都是和声,但和声不一定会产生拍音。
具体区别:
- 人耳可以听到的声波频率范围大约为$20\rm Hz$到$20000\rm Hz$,如果和声产生的频率超过这个范围,通常就不能称之为拍音了。
- 不同的乐器发出的单音进行叠加也可以称为和声,这也不是拍音。拍音要求所有单音同时发出,而和声则无此要求,只要一个音在另一个音结束之前发出,它们交叠的部分就形成了和声。
在西方古典音乐理论中,和声主要研究两个单音构成的和声,三个或以上单音构成的和声一般称为和弦,我们放在下一节讨论。在一个纯八度范围内,两个单音的和声一共有$12$种,即与$12$种音程相对应。在钢琴键盘上以中央$C$键,即$C4$为准,请试听一下$C4$分别与$D4$、$E4$、$F4$、$G4$、$A4$、$B4$以及$C5$键同时按下的和声效果。
听过以后,发现某些和声比较悦耳,而某些则比较难听。
比如$C4$和$C5$同时按下(纯八度音程)的和声就婉如只有一个音,十分融洽;而$C4$和$D4$同时按下(小二度音程)就使人非常难受。这是为什么呢?

就是因为拍音!
相邻两个音之间的频率比为$\sqrt[12]{2}\approx 1.059463$,我们将这个数记为$p$,那么各音程的频率比(即相距某个音程的低音比高音)可由其音数$t$按公式:$\dfrac{1}{ (2t) ^ p }$算得。由于除纯八度外的所有音程的频率比均为无理数,因此他们的拍音的频率只能按他们频率的近似整数比来计算,详见第一讲第三节。计算近似整数比的数学过程是比较复杂的,这里篇幅有限,不做进一步的讨论。接下来我们分别换算一下$12$个音程的频率比。
| 音程 | 近似频率比 | 近似整数比 | 最小公倍数 |
|---|---|---|---|
| 小二度 | $1:1.06$ | $15:16$ | $240$ |
| 大二度 | $1:1.12$ | $8:9$ | $72$ |
| 小三度 | $1:1.19$ | $5:6$ | $30$ |
| 大三度 | $1:1.26$ | $4:5$ | $20$ |
| 纯四度 | $1:1.34$ | $3:4$ | $12$ |
| 三全音 | $1:1.41$ | $7:10$ | $70$ |
| 纯五度 | $1:1.50$ | $2:3$ | $6$ |
| 小六度 | $1:1.59$ | $5:8$ | $40$ |
| 大六度 | $1:1.68$ | $3:5$ | $15$ |
| 小七度 | $1:1.78$ | $5:9$ | $45$ |
| 大七度 | $1:1.89$ | $8:15$ | $120$ |
| 纯八度 | $1:2$ | $1:2$ | $2$ |
按近似整数比的最小公倍数排序,可以得到如下和声序列:
纯八度,纯五度,纯四度,大六度,大三度,小三度,小六度,小七度,三全音,大二度,大七度,小二度
通过在钢琴上弹奏对比可知,越向左边的和声越协和,但也越空洞,就是好像只有一个音,不够饱满;越向右边的和声越难听,但也越饱满。人们根据这一特征,将和声的协和程度分为极完全协和、完全协和、不完全协和、不协和与极不协和这五类,如下图所示:

我们做一个实验来验证。
- 比如$C4$和$G4$之间是完全协和的纯五度,他们的弦长比是$3:2$,最小公倍数是$6$,那么他们的拍音频率就是弦长为$C4$弦长$2$倍的弦所发出的声音的频率,显然就是$C3$的音。
- 可以在钢琴上面按$C4,G4,C3$,可以感觉到$C4$和$G4$把$C3$增强了。同理,$A6$和$B6$这两个小二度音程的弦长比是$16:15$,最小公倍数$240$,拍音频率对应的音为$B2$,然而$B2$与$A6$和$B6$相隔太远了,我们无法听出拍音增强的效果。
PS: 和声理论已经发展为一门学科,称为和声学,内容是相当复杂的,这里只做简单介绍,感兴趣的可以阅读《和声学》,下面给出一份参考pdf:音乐自学丛书·和声学基础教程
