基础乐理与数学(一)
声学基础
乐理的基本内容包括:和声、调式、节奏、结构、曲式。主要来说,音乐的组成从简单到复杂依次是:纯音、谐波、拍音、和声、调式、曲式。下面只介绍前几种基本的音乐组成单元。
音与音的复合
- 音:
能被人类的听觉所感知的一段声波,通常可以用一个声波的波形来表示。
音的本质是一段声波(根据人耳辨别范围可知声波频率应在$20{\rm Hz} -20000\rm Hz$之内)。
一般音乐中的每个音都是周期性的,这在后面音的谐和部分会提到。
音是可以叠加的,后一个音出现时,前一个音可能尚未消失,这就关联到声波方面的傅立叶变换。音是音乐的最基本的组成单位。
- 音的复合:
说到声波最先想到的最简单的波形即是正弦波,即以某个固定频率进行简谐振动所产生的声波。
这种声波被称为纯音,比如音叉的声音或$220\rm Hz$正弦波。
纯音显然几乎没有音色可言,音与音的复合形成了复合音。
复合音一般分为两种:谐波叠加与拍音叠加。
谐波叠加与拍音叠加
将一个标准的正弦波作为基准,称作基波。谐波就是比基波的频率高整数倍的波,钢琴按下一个键或小提琴拉响一根弦都会在基波的基础上产生多个谐波,音乐人往往将谐波称为泛音。例如某个纯音声波的频率是$f$,将此纯音作为基波,其谐波的频率可为$2f$、$3f$、$4f$、……,这些谐波分别称为二次谐波、三次谐波、四次谐波等。如下图所示。
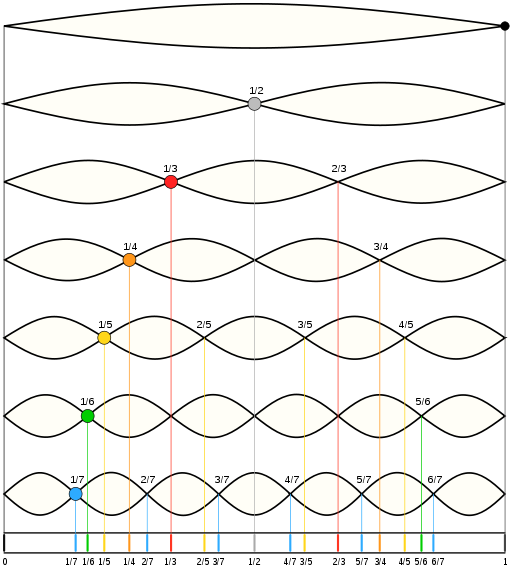
最上面的是基波,从第二行往下分别是一次谐波、二次谐波等等。若一个复合音由基波与及其谐波相叠加构成,则称该复合音为谐波叠加,它的频率为基波频率。基波与谐波叠加构成复合音的过程见图3所示。
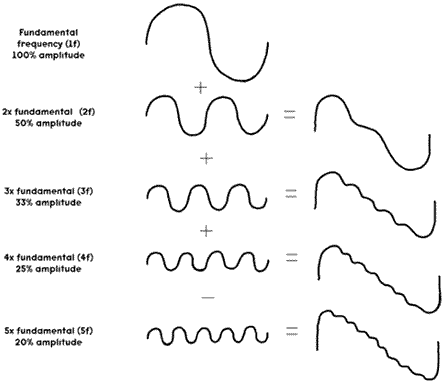
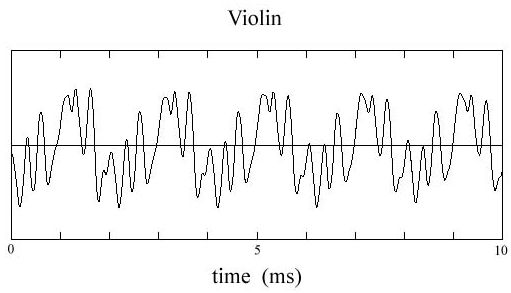
实际上,所有传统乐器所发出的音都是复合音,由振幅最大的基波和一些列振幅较小的谐波叠加构成。那么我们就可以给出单音的定义了:单音特指单一乐器演奏独立的一个音发出的声波(谐波叠加),其基波的频率称为音高。不同乐器的单音所叠加的谐波在频率和振幅上都不相同,因此乐器的音色千差万别。小提琴的单音就是典型的一种谐波叠加,声音对应的波型为:
- 谐波叠加
我们将一个标准的正弦波作为基准,称为基波,谐波就是比基波的频率高整数倍的波。钢琴、小提琴等弦乐器产生的一个音一般都是多个谐波的叠加,在音乐领域被称为泛音。一般将一个音中振幅最大的波作为基波,其余波的频率都是这个波的倍数。
也就是说,组成一个谐波叠加的音的所有正弦波$k\sin(x \omega)$的频率都是基波的倍数。
- 拍音叠加
一个拍音是由来自同一种乐器或不同乐器的两个单音相互叠加,形成具有规律性强弱变化的振动。与谐波不同的是,拍音一般要求这两个音的振幅相近,但不要求频率为倍数关系。粗略理解就是:如果组成复合音的纯音频率互为倍数则为谐波叠加,否则为拍音叠加。
- 复合音的频率与“谐和”
只考虑最简单的情况,两个音的频率分别为$a$和$b$,则这两个音的叠加的频率应为多少?
复合音的周期是这两个音的周期的最小公倍数,即$\gcd\left ( \dfrac{1}{a},\dfrac{1}{b} \right )$,频率即为周期的倒数。
但是,如果两个音的频率均为无理数,例如$\sqrt{3}$与$\sqrt{5}$,理论上这不是一个周期函数,这时需要用到近似。这个复合音的频率可以认为是$\dfrac{1}{4\sqrt{3}}$,因为$\dfrac{ \sqrt{3} }{ \sqrt{5} } \approx 0.7746$,接近于$0.75$,也就是$3:4$。因此这个拍音的“听感频率”大约在$\dfrac{\sqrt{5}}{4}$到$\dfrac{\sqrt{3}}{3}$之间。
人耳一般会认为复合音的频率越高,声音越悦耳,即两个音的频率的倒数的最小公倍数应尽量小,这样的两个音被称为彼此谐和的。
这里出现了一个数学方面的拓展:复合音的频率与测度论的关系。
乐律与调式
十二平均律
- 平均律
首先我们要知道,跨越一个八度音程的两个音的频率相差一倍,即$a:b=1:2$。
现在我们将一个八度音程等分成十二个部分,那么显然第一个音是$a$,第二个音是$\displaystyle a\cdot 2^\frac{1}{12}$,第三个是$\displaystyle a\cdot 2^\frac{2}{12}$,…,第十三个是$2a$。
十二平均律中,任意两个相邻的音的频率比为$2^\frac{1}{12}$任两个相邻的音之间的音数为$0.5$。
- 音程名称与音数
学过乐理的人一定能辨别每两个音相差的音程名称,而每个音程名称都对应了一个固定的音数,如下表:
| 相差音数 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 音程名称 | 小二度 | 大二度 | 小三度 | 大三度 | 纯四度 | 三全音 | 纯五度 | 小六度 | 大六度 | 小七度 | 大七度 | 纯八度 |
- 五线谱
需要注意的是,第一个音程的$A$音的频率是$440\rm Hz$,这样我们就可以轻松地计算出任何一个音的频率了。
五度相生律
前面提到,人们一般会认为两个彼此谐和的音之间会较为悦耳,但我们遗憾地发现,用十二平均律规定的各个音大部分都是完全不谐和的,这使人们希望找到一个彼此更加谐和的划分方法。
我们将一个弦分成$1:2$两部分,则这两部分的频率比为$3:2$,如果在前$\dfrac{1}{3}$中再分出前,则$\dfrac{1}{3}$两部分的频率比变为$\dfrac{9}{4}$,以此类推,我们将这个频率列成表:
| $n$ | 频率 | 倍率 |
|---|---|---|
| $1$ | $\dfrac{3f}{2}$ | $1.5$ |
| $2$ | $\dfrac{9f}{4}$ | $2.25$ |
| $3$ | $\dfrac{27f}{8}$ | $3.375$ |
| $4$ | $\dfrac{81f}{16}$ | $5.0625$ |
| $5$ | $\dfrac{243}{32}$ | $7.59375$ |
这个倍率已经超过$2$了,那么我们将每个值除以不大于它的最接近的$2$的次幂,从小到大排列:$\{1.125, 1.265625 ,1.333, 1.5, 1.6875, 1.8984375\}$。$f$自身的倍率为$1$,$2f$为$2$,把这$8$个倍率一起画在二维坐标系中,如图所示。
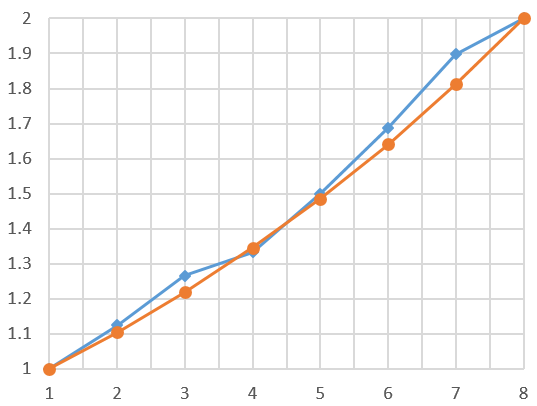
这个和呈完美指数增长的划分相差并不多,更奇妙的是,由刚才的推导,这些音两两谐和。
纯律
我们在五度相生律中取得了良好的效果,继续这个思路,接着将表列出来:
| n | 频率 | 倍率 |
|---|---|---|
| $1$ | $\dfrac{3}{2}$ | $1.5$ |
| $2$ | $\dfrac{9}{4}$ | $2.25$ |
| $3$ | $\dfrac{27}{8}$ | $3.375$ |
| $4$ | $\dfrac{81}{16}$ | $5.0625$ |
| $5$ | $\dfrac{243}{32}$ | $7.59375$ |
| $6$ | $\dfrac{729}{64}$ | $11.3906$ |
| $7$ | $\dfrac{2187}{128}$ | $17.0859$ |
| $8$ | $\dfrac{6561}{256}$ | $25.6289$ |
| $9$ | $\dfrac{19683}{512}$ | $38.4434$ |
| $10$ | $\dfrac{59049}{1024}$ | $57.6650$ |
| $11$ | $\dfrac{177147}{2048}$ | $86.4976$ |
由这些倍率产生的12音阶为(用倍率除以它下面的第一个$2^n$而得):$\{1, 1.0679, 1.125, 1.2014, 1.2656, 1.3515, 1.4238, 1.5, 1.6018, 1.6875, 1.802, 1.8984\}$,把他们画在坐标系中:
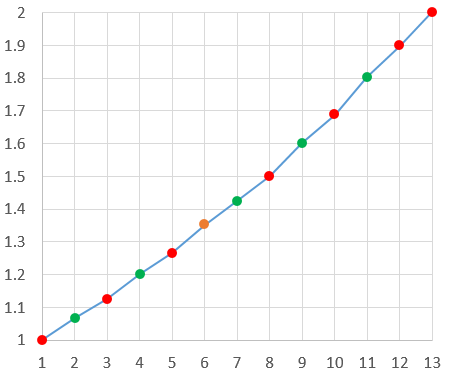
五度相生律产生$12$音阶(新产生的五个音为绿色)
这也是一条平滑的折线,且每个音两两谐和,这就是纯律。
